1. Fungsi Biaya dan Fungsi Penerimaan
1.1. Fungsi Biaya
Biaya total (total cost) yang dikeluarkan oleh sebuah perusahaan dalam operasi bisnisnya terdiri atas biaya tetap (fixed cost).
Sesuai dengan namanya, sifat biaya tetap adalah tidak tergantung pada
jumlah barang yang dihasilkan. Berapa unitpun barang yang dihasilkan,
jumlah biaya tetap dalam jangka pendek senantiasa tidak berubah. Secara
matematik, biaya tetap bukan merupakan fungsi dari jumlah barang
dihasilkan tetapi merupakan sebuah konstanta, dan kurvanya berupa sebuah
garis lurus sejajar sumbu jumlah. Sebaliknya biaya variabel tergantung
pada jumlah barang yang dihasilkan. Semakin banyak jumlah barang yang
dihasilkan semakin besar pula biaya variabelnya. Secara matematik biaya
variabel merupakan fungsi dari jumlah barang yang dihasilkan, kurvanya
berupa sebuah garis lurus berlereng positif dan bermula dari titik
pangkal.
FC = k
VC = f (Q) = vQ
C = g (Q) = FC + VC = k + vQ
Keterangan :
FC : biaya tetap
VC : biaya variabel
C : biaya total
k : konstanta
Contoh 6 :
Biaya
tetap yang dikeluarkan oleh sebuah perusahaan sebesar Rp. 20.000,-
sedangkan biaya variabelnya ditunjukkan oleh persamaan VC = 100Q.
a. Tunjukkan persamaan dan kurva biaya totalnya!
b. Berapa biaya total yang dikeluarkan jika perusahaan tersebut memproduksi 500 unit barang ?
Jawab :
b. Jadi perusahaan harus mengeluarkan biaya total sebesar Rp. 70.000,0 untuk memproduksi 500 unit barang.
1.2. Fungsi Penerimaan
Penerimaan sebuah perusahaan dari hasil penjualan barang merupakan
fungsi dari jumlah barang yang terjual atau dihasilkan. Semakin banyak
barang yang diproduksi dan terjual semakin besar pula penerimaannya.
Penerimaan total (total revenue) adalah hasil kali jumlah barang
yang terjual dengan harga jual per unit barang tersebut. Secara
matematik, penerimaan merupakan fungsi jumlah barang kurvanya berupa
garis lurus berlereng positif dan bermula dari titik pangkal.
R = Q x P = f (Q)
dalam
menganalisis penerimaan selalu dianggap bahwa perusahaan senantiasa
berhasil menjual setiap barang yang dihasilkannya, dengan demikian Q
dalam R = f (Q) bukan saja melambangkan jumlah barang dihasilkan tetapi
juga melambangkan jumlah barang yang terjual.
Contoh 7 :
Harga jual produk yang dihasilkan oleh sebuah perusahaan Rp. 200,- per unit.
a. Tunjukkan persamaan dan kurva penerimaan total perusahaan tersebut !
b. Berapa besar penerimaannya bila terjual barang sebanyak 350 unit ?
Jawab :
R = Q x P
= Q x 200 = 200 Q
b. Bila Q = 350, maka R = 200 x 350 = 70.000
2. Analisis Pulang Pokok (Break Even Point)
Penerimaan
dan biaya merupakan variabel-variabel penting untuk mengetahui kondisi
bisnis suatu perusahaan. Bila diketahui penerimaan total (R) yang
diperoleh dari biaya total (C) yang dikeluarkan, maka dapat dianalisis
apakah perusahaan mendapat keuntungan atau mengalami kerugian.
Keuntungan (profit positif, ….> 0) akan didapat bila R > C, secara grafik hal ini terlihat pada area dimana kurva R terletak di atas kurva C. Sebaliknya
kerugian (profit positif, ….< 0) akan didapat bila R < C, secara
grafik hal ini terlihat pada area dimana kurva R terletak di bawah kurva
C.
Konsep yang lebih penting berkenaan dengan R dan C adalah konsep
“pulang pokok (break even point)” yaitu konsep yang digunakan untuk
menganalisis jumlah minimum produk yang harus dihasilkan atau terjual
agar perusahaan tidak mengalami kerugian. Keadaan pulang pokok (profit
nol, …..=0) terjadi apabila R = C, artinya perusahaan tidak memperoleh
keuntungan tetapi tidak pula merugi. Secara grafik hal ini ditunjukkan
oleh perpotongan antara kurva R dan C.

Q*
mencerminkan posisi tingkat produksi/penjualan pulang pokok. Area
disebelah kanan Q* merupakan area keuntungan (….>0) sedangkan di
sebelah kiri Q* merupakan area kerugian (…. < 0).
Contoh 8 :
Bila
biaya total yang dikeluarkan perusahaan ditunjukkan oleh persamaan
C=20.000+100Q dan penerimaan totalnya R = 200Q. Pada tingkat produksi
berapa unit perusahaan ini berada dalam posisi pulang pokok ? Apa yang
terjadi jika perusahaan tersebut berproduksi sebanyak 300 unit ?
Jawab :
Kondisi pulang pokok akan terjadi apabila ….=0, dimana nilai …= R – C. Artinya R – C = 0 atau R = C.
R =C
200Q = 20.000 + 100Q
100Q = 20.000
Jika Q = 300 unit maka,
R = 200 (300) = 60.000;
C = 20.000 + 100(300) = 50.000
…..= R – C = 60.000 – 50.000 = 10.000
Jadi
apabila perusahaan memproduksi sebanyak 300 unit maka perusahaan akan
memperoleh keuntungan sebesar 10.000. Posisi pulang pokok terjadi pada
tingkat produksi 200 unit, R dan C sama-sama sebesar 40.000.
3. Fungsi Anggaran
Ekonomi mikro mengenal dua teori yang membahas tentang fungsi anggaran yaitu teori produksi dan teori konsumsi. Pada teori produksi, fungsi anggaran mencerminkan batas maksimum kemampuan seorang produsen membeli dua macam input atau lebih, berkenaan dengan jumlah dana yang tersedia dan harga masing-masing input. Gambar dari fungsi anggarannya dikenal dengan sebutan isokos (isocost). Pada teori konsumsi, fungsi anggaran mencerminkan batas maksimum kemampuan seorang konsumen membeli dua macam output atau lebih, berkenaan dengan jumlah pendapatannya dan harga masing-masing output. Gambar dari fungsi anggarannya dikenal dengan sebutan garis anggaran (budget line).
Bentuk umum persamaan fungsi anggaran,
M = x. Px + y. Py
Teori Produksi
|
Teori Konsumsi
|
M : jumlah dana produsen
x : jumlah input X
y : jumlah input Y
Px : harga X per unit
Py : harga Y per unit
|
M : jumlah pendapatan konsumen
x : jumlah output X
y : jumlah output Y
Px : harga X per unit
Py : harga Y per unit
|
Contoh 9 :
Bentuklah
persamaan anggaran seorang konsumen untuk barang X dan barang Y apabila
pendapatan yang disediakannya sebesar Rp. 100.000,- sedangkan harga
barang X dan barang Y masing-masing Rp. 500,- dan Rp. 1.000,- per unit.
Jika semua pendapatan yang dianggarkan dibelanjakan untuk barang X,
berapa unit barang X dapat dibelinya ?. Berapa unit barang Y dapat
dibeli kalau ia hanya membeli 100 unit barang X ?
Jawab :
M = x. Px + y. Py
Persamaan anggarannya adalah 100.000 = 500 X + 1000 Y.
Jika
semua pendapatan dibelanjakan untuk barang X ( Y = 0), maka jumlah X
yang dapat dibeli 100.000 = 500 X —› X = 200 unit. Jika barang X dibeli
sebanyak 100 unit maka,
100.000 = 500 (100) + 1000 Y
1000 Y = 50000
Y = 50 unit







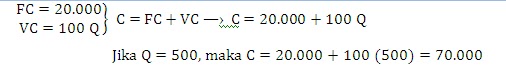





 Time in Ambon
Time in Ambon
Ini bagus materinys
BalasHapus